LISTRIK STATIS
Petir adalah suatu kejadian alam yang luar biasa, karena dalam setiap kejadiannya energi yang dilepaskan lebih besar daripada yang dihasilkan oleh seluruh pusat pembangkit tenaga listrik di Amerika. Cahaya yang dikeluarkan oleh petir lebih terang daripada cahaya 10 juta bola lampu pijar berdaya 100 watt. Hal lain yang menakjubkan bahwa molekul-molekul nitrogen, yang sangat penting untuk tumbuhan, muncul dari kekuatan ini.Mengapa petir dapat membebaskan energi? Darimana petir mendapatkan energi listrik?
Berapa biaya listrik yang dapat kita hemat jika kita dapat mengumpulkan energi dari petir?
Saat kita merenungi semua perihal petir ini, kita dapat memahami bahwa peristiwa alam ini adalah sesuatu yang menakjubkan. Bagaimana sebuah kekuatan luar biasa semacam itu muncul dari partikel bermuatan positif (proton) dan negatif (elektron) dari dalam sebuah atom, yang tak terlihat oleh mata telanjang. Perbedaan jumlah proton dan elektron dalam sebuah atom mengakibatkan atom bermuatan listrik. Karena semua benda tersusun oleh atom-atom, maka perubahan muatan listrik pada atom akan mengakibatkan perubahan listrik pada benda.
Setiap benda memiliki kecenderungan untuk berada dalam keadaan netral, oleh karena itu jika benda bermuatan maka secara spontan dapat membebaskan muatannya. Salah satu contohnya adalah petir. Sifat-sifat muatan listrik antara lain: 1) listrik terdiri dari dua jenis muatan yaitu muatan positif dan negatif, 2)muatan listrik akan saling berinteraksi, muatan sejenis tolak menolak dan muatan tidak sejenis tarik-menarik. Para ahli berusaha memanfaatkan muatan listrik statis untuk berbagai keperluan dalam kehidupan sehari-hari.
Bagaimana Benda dapat Bermuatan Listrik?
Setiap zat tersusun atas atom-atom, dengan demikian muatan listrik suatu zat tergantung dari jenis muatan listrik atom-atomnya. Jika atom-atom benda lebih cenderung melepaskaan elektron, maka zat yang disusunnya lebih cenderung bermuatan positif. Sebaliknya jika atom-atom benda lebih cenderung menangkap elektron, maka zat yang disusunnya cenderung bermuatan negatif. Dengan demikian muatan listrik sebuah benda sangat tergantung dengan muatan listrik atom-atom penyusunnya.
Bagaimana cara membuat benda bermuatan listrik?
Suatu benda dapat dimuati listrik dengan dua cara yaitu:
1. Menggosok
a. Menggosok penggaris plastik dengan kain wool --> Penggaris menjadi bermuatan listrik jenis negatif.
b. Menggosok kaca dengan kain sutera --> Kaca menjadi bermuatan listrik jenis positif.
Mengapa dengan menggosokkan benda ke benda lain dapat membuat benda bermuatan listrik? Apakah semua benda jika digosokkan akan bermuatan listrik?
Muatan listrik pada sebuah benda, sangat dipengaruhi olah muatan listrik atom-atom penyusunnya. Ada atom-atom yang cenderung melepas elektron, tetapi ada juga atom-atom yang cenderung mengikat elektron. Jika dua benda tersusun dari atom-atom yang memiliki perbedaan sifat tersebut saling digosokkan maka, maka interaksi itu akan lebih mudah membuat benda bermuatan listrik.
Dari animasi di atas. Jika kain sutera digosokkan pada kaca, maka elektron-elektron kaca akan berpindah menuju sutera, sehingga kaca menjadi bermuataan positif. sementara itu kain sutera menjadi bermuatan negatif karena mendapat tambahan elektron.
Jika kain wool digosokkan pada plastik, maka elektron-elektron kain wool akan berpindah menuju plastik, sehingga plastik menjadi bermuataan negatif. sementara itu kain wool menjadi bermuatan positif karena kehilangan elektron-elektronnya.
2. Induksi
Bagaimana proses pemuatan listrik dengan induksi?
Induksi dapat dilakukan dengan cara mendekatkan benda yang bermuatan listrik ke benda netral. Akibatnya benda netral akan terpolarisasi. Jika benda netral yang telah terpolarisasi di hubungkan dengan tanah (di ground kan), maka elektron-elektronnya akan mengalir menuju tanah. Setelah penghantar yang menuju tanah di hilangkan dan benda bermuatan listrik dijauhkan, maka benda netral akan menjadi kekurangan elektron (bermuatan positif). Induksi dalam jumlah muatan tertentu dapat mengakibatkan muatan listrik melompati gap (jarak pemisah), dalam hal ini dapat menimbulkan lintasan bunga api. Salah satu peristiwa yang besar adalah terjadinya petir.
Sifat Muatan Listrik --> Muatan listrik dapat menarik benda-benda kecil
Potongan kertas kecil-kecil dapat menempel pada penggaris yang bermuatan listrik karena adanya gaya listrik. Jika gaya listrik lebih besar dari gaya gravitasi benda maka benda akan menempel pada penggaris, sebaliknya jika gaya listrik kurang dari gaya gravitasi, maka benda tidak akan menempel.
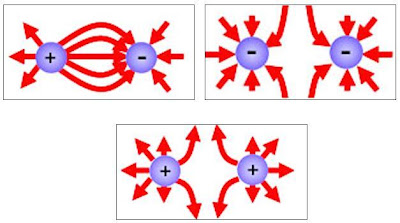
Interaksi antara dua muatan listrik baik berupa gaya tolak atau gaya tarik dapat digambarkan dengan menggunakan garis-garis gaya listrik berikut: